| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- CoreBluetooth
- DiffableDataSource
- DependencyInjection
- swift
- SRP
- combine
- IOS
- data_structure
- rxswift
- baseviewcontroller
- cleanarchitecture
- 오픈채팅방
- leetcode
- GCD
- DispatchQueue
- 명품cppProgramming c++
- 프로그래머스
- MethodSwilzzling
- RaceCondition
- SeSAC
- 청년취업사관학교
- 코테
- SwiftUI
- MainScheduler.asyncInstance
- Realm
- MainScheduler.Instance
- MainScheduler
- gitflow
- 등굣길
- DynamicMemberLookup
- Today
- Total
Do.
Data Structure - Heap (w/Swift) 본문
What is Heap
힙은 완전 이진 트리 기반의 자료 구조입니다. 구현 하기 위해서는 트리가 어떤 형태를 가지고 있는 자료 구조인지 미리 알면 좋을 것 같습니다.
힙은 일반적으로 두가지 힙이 있습니다. Max Heap과 Min Heap이 있습니다. 최대 힙은 말 그대로 큰 수가 가장 우선 순위가 높고, 최소 힙은 작은 수가 우선 순위가 높습니다.
우선 순위라는 말을 썼는데요!, Heap 자료 구조는 Priority Queue 자료 구조를 만들 때 활용할 수 있습니다!
힙 자료구조는 어떻게 만들고, 데이터 삽입, 출력은 어떻게 하는지 알아 보도록 하겠습니다.
Building
Heap은 우선 데이터를 삽입 하고 제거할 때, Tree 형태 자료에 맞게 재배치를 하는 과정이 필요합니다. Max-Heap 기준으로 설명하자면
데이터를 삽입하면 자신이 있어야 할 위치까지 재배치 하는 과정이 필요하다는 거죠! 예를 들어 볼게요!
remove

힙에서 제거가 어떤 식으로 이루어 지는지 먼저 봐보겠습니다. 우선 Max-Heap에서는 가장 큰 수가 먼저 나온다고 말씀드렸죠.
그러면 10이 remove 동작을 하게 될 경우 가장 먼저 나와야 합니다.
힙은 내부적으로 배열로 구현되는데요! 10을 빼겠다고 removeFirst()를 하게되면 배열을 재배치 하는 과정에서 O(n)이라는 시간이 발생하고 맙니다!
따라서 배열의 가장 마지막 요소를 제거하면 가장 빨리 제거할 수 있죠!
그래서 가장 첫번 째 요소와 가장 마지막 요소를 우선 Swap 합니다.

5와 10을 바꾸었네요!, 이제 10은 가장 마지막에 있으니 꺼내주면 됩니다.
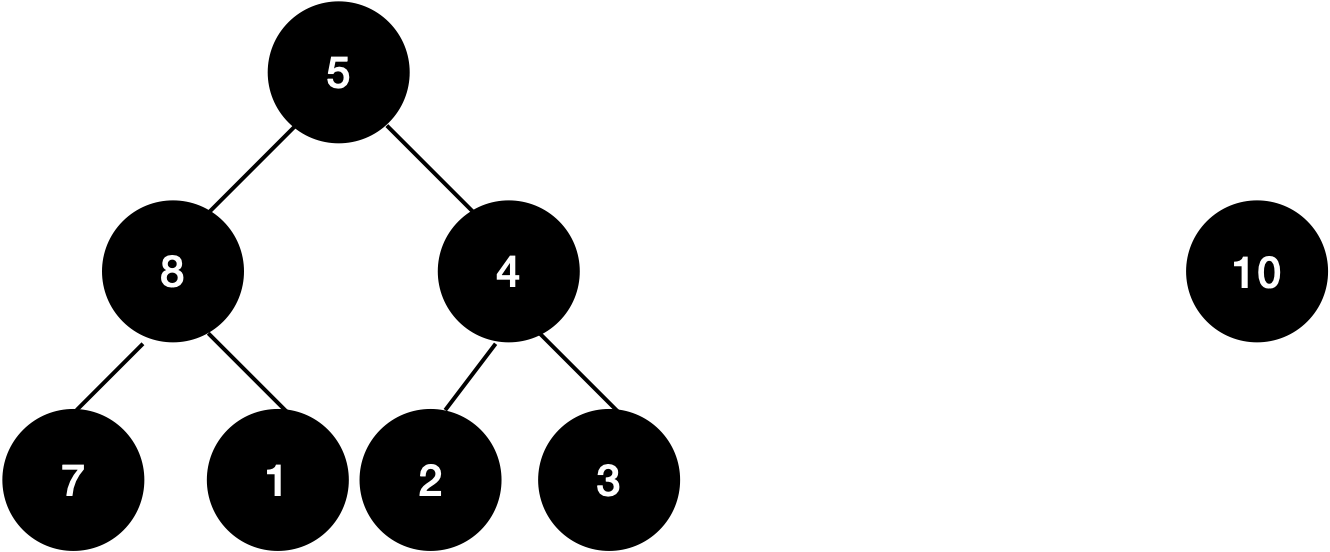
힙에서 가장 우선 순위가 높은 값(10)을 얻었네요, 그런데 여기서 멈추면 Max-heap 구조가 무너지기 때문에 재배치 하는 과정을 거칩니다.
재배치 과정은 어렵지 않습니다. 자식 노드 두개를 비교해서 자신 보다 큰 노드와 위치를 바꿔주면 됩니다. 만약 자신 보다 자식 노드 둘다 크다면 더 큰 노드와 바꿔주면 됩니다.
즉 다음 동작은 5를 8과 4와 비교하여 더 큰값과 바꿔주면 됩니다.

8과 5를 바꾸었죠? 4는 5보다 작기 때문에 대상이 아닙니다. 이제 이 동작을 5에 대해서 더이상 교체할 노드가 없을 때 까지 반복해 주면 됩니다.
그러니까 그 다음은 5를 7과 1을 비교해서 더 큰 값과 바꿔주면 됩니다. 7과 바꿔주면 되겠네요!
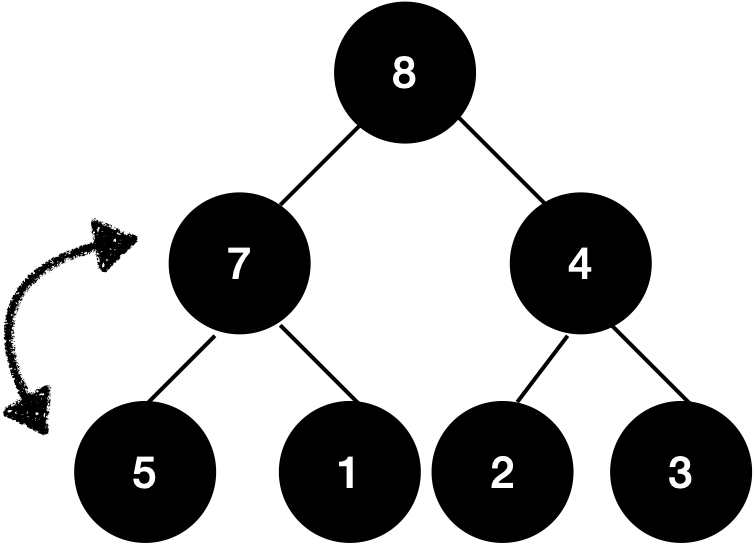
이제는 더 바꿀 노드가 없으므로, 이렇게 되면 이 Heap은 다시 Max-Heap 구조가 완성 되었습니다. 이 과정을 sift-down이라고 합니다. 여기서 트리 구조만 보고서는 이게 정렬이 된건가 의아해 하실 수도 있는데요, 그 다음 큰 값을 제거 해볼까요?

8을 빼기 위해서 가장 마지막 노드와 자리를 바꿔준 다음 8을 빼줍니다. 그런 다음 3을 sift-down 해볼게요

3을 7,4와 비교해서 더 큰값인 7과 바꿔 준 다음

그 다음 3의 자식 노드인 5, 1과 비교해서 더 큰 값인 5과 변경 해줍니다.

3은 더 이상 자식 노드가 없으니 sift-down이 끝났죠?
그 다음 큰값을 빼게 되면

7과 2를 swap 하고 7을 내보 낸 뒤 2를 sift-down 합니다.
2를 5,4와 비교하여 가장 큰 값인 5와 바꿔주고, 그 다음 2의 자식인 3,1과 비교하여 더 큰값인 3과 바꿔 줍니다.


그 다음 큰 값인 5가 빠질려면 1과 swap 하게 되고 1로 sift - down을 합니다. 이 때 1의 자식인 3,4를 비교해서 더 큰 값인 4와 바꾸게 되면 1의 여정은 끝이나죠
이 과정은 노드가 다 없어질 때 까지 반복하다 보면

가장 큰 순서대로 값이 빠져나온 것을 볼 수 있습니다!
insert
값을 삽입 하는 방법은 sift-down 이 아닌 sift-up을 하면 됩니다. 마찬가지로 갑 추가는 트리의 가장 마지막 노드에 추가하고, 이를 sift-up하면서 올라가면 됩니다. sifu-up은 sift-down보다 더 쉬운데요! sift-down은 두 자식 노드 중 더 큰 값과 변경 해주는 반면, sift-up은 부모 노드가 자신 보다 더 작으면 무조건 바꿔주면 됩니다. 비교 할 대상이 하나 뿐인 것이죠 (max-heap 기준)
Implementation
이제 실제로 Swift 언어로 구현해봅시다.
struct Heap<T: Equatable> {
private var elements: [T] = []
private let sort: (T, T) -> Bool
init(sort: @escaping (T, T) -> Bool) {
self.sort = sort
}
}우선 Heap을 배열로 구현할 거라고 말씀 드렸습니다. 따라서 내부 데이터로 배열을 가지고 있을 겁니다.
타입은 제네릭 T로 표현할 것이고, sift-up, sift-down 할때 두 값을 비교해서 누가 더 큰지 알아야 했기 때문에, Equatable을 준수하는 타입으로 제약을 걸겠습니다.
sort라는 함수 타입을 통해 최대 힙인지, 최소 힙인지 구분할 수 있기 때문에 이를 생성 시점에 받도록 하겠습니다. 무슨 소리냐 하면
Sift-down 할 대 부모 노드와 자식 노드를 비교를 하잖아요? lhs값이 부모고, rhs값이 자식일 때 자식이 부모보다 클 때 즉 lhs > rhs이면 최대 힙 조건에 맞게 구성이 됐었기 때문에, sort라는 함수타입에 >를 전달해 주면 최대 힙이 되는 것이고 <를 전달해 주면 최소 힙이 되는겁니다.
Child Node Index
Heap에서 Sift-down, up 할 때 자식 노드와 부모 노드의 인덱스를 Swap 했잖아요? 즉 자식 노드와 부모노드의 인덱스를 알아낼 방법이 필요합니다.
트리는 다음과 같은 형태로 순번을 가지죠?,

예를들어 1번 노드(값 8) 를 부모 노드라고 했을 때 자식 노드의 인덱스는 3, 4입니다.
즉 왼쪽 자식 노드는 p * 2 + 1 이고 오른쪽 자식 노드는 왼쪽 자식 노드의 무조건 그 다음 이기 때문에 L + 1과도 같습니다.
따라서 다음 두 인스턴스 메서드를 추가합니다.
private func leftChildIndex(parent: Int) -> Int {
parent * 2 + 1
}
private func rightChildIndex(parent: Int) -> Int {
parent * 2 + 2
}그 다음 가장 높은 우선 순위 값을 빼는 순서를 말씀 드렸죠.
0번과 가장 마지막 노드를 swap 한 다음 마지막 값을 빼 내고, sift-down이라는 것을 수행 하면 됩니다.
mutating
func remove() -> T? {
guard !isEmpty else { return nil }
elements.swapAt(0, count - 1)
defer {
siftDown(start: 0)
}
return elements.removeLast()
}이러한 코드겠죠, swapAp을 하기 위해서는 1이상의 개수가 필요하므로 0개일 때는 조기 종료문을 써줍니다!
siftDown 메서드는 아직 작성하지 않았죠?
해당 메서드에 포함되어야 할 내용은 크게 어렵지 않습니다.
왼쪽 자식 노드와 오른쪽 자식 노드와 비교해서 더 큰값과 위치를 바꿉니다.
이 동작을 더이상 바꿀 자식 노드가 없을 때 까지 반복하면 됩니다.
mutating
private func siftDown(start: Int) {
var parent = start
var candidate = parent
while true {
let leftChild = leftChildIndex(parent: parent)
let rightChild = rightChildIndex(parent: parent)
if leftChild < count, sort(elements[leftChild], elements[candidate]) {
candidate = leftChild
}
if rightChild < count, sort(elements[rightChild], elements[candidate]) {
candidate = rightChild
}
if parent == candidate {
return
}
elements.swapAt(parent, candidate)
parent = candidate
}
}이제 삽입 메서드를 만들어 보겠습니다.
삽입은 말씀 드렸던 순서대로, 트리 마지막에 새 값을 추가 한뒤 sift-up이라는 동작을 수행하면 된다고 말씀드렸습니다.
mutating
func insert(_ element: T) {
elements.append(element)
siftUp(start: count - 1)
}siftUp을 구현하기 전에 부모 노드의 인덱스를 알아낼 방법을 찾아보겠습니다.

이번에는 자식 노드를 기준으로 보니까 3번 노드(값 5) 를 볼까요?
3번의 부모 노드 인덱스는 1이므로 (3 - 1) / 2 를 하면 1이 나오겠네요! 4번 노드의 입장에서도 같습니다. (4 - 1) / 2을 하면 1이 나오네요!
즉 (C - 1) / 2 를 하면 부모 노드의 인덱스를 구할 수 있습니다.
private func parentIndex(child: Int) -> Int {
(child - 1) / 2
}요렇게 쓰면 되겠습니다!
이제 다시 sift-up을 작성하러 가볼까요!
mutating
private func siftUp(start: Int) {
var child = start
var parent = parentIndex(child: child)
while child > 0, sort(elements[child], elements[parent]) {
elements.swapAt(parent, child)
child = parent
parent = parentIndex(child: child)
}
}
이제 기본 적인 모양새는 갖추었으니 실제로 써볼까요?
var heap = Heap<Int>(sort: >)
heap.insert(1)
heap.insert(7)
heap.insert(4)
heap.insert(10)
heap.insert(2)
while let value = heap.remove() {
print(value)
}무작위로 숫자를 넣어주고
heap을 반복해서 remove 해주면

촤란~ Max Heap이 완성 되었습니다.
Additional
있으면 좋은 추가 기능을 작성해볼려고 합니다.
임의의 노드를 제거 해볼 수 있을텐데요! 이때는 어떻게 해야 할까요?
어렵지 않습니다. 해당 노드의 인덱스를 힙의 마지막 노드의 인덱스와 swap 해 준 뒤 선택한 인덱스 위치로부터 sift-up과 sift-down을 수행해주면 됩니다.
mutating
func remove(at index: Int) -> T? {
guard index < count else { return nil }
if index == count - 1 {
return elements.removeLast()
} else {
elements.swapAt(index, count - 1)
defer {
siftDown(start: index)
siftUp(start: index)
}
return elements.removeLast()
}
}어렵지 않습니당. 그런데 제거하려는 노드가 어느 인덱스에 있는지는 어떻게 찾을까요?
루트 노드 부터 시작해서 왼쪽, 오른쪽 자식을 모두 뒤지는 수 밖에는 없습니다. 재귀 함수로 구현 해 볼게요
func index(of element: T) -> Int? {
index(of: element, startingAt: 0)
}
private func index(of element: T, startingAt i: Int) -> Int? {
if i >= count {
return nil
}
if sort(element, elements[i]) {
return nil
}
if element == elements[i] {
return i
}
if let j = index(of: element, startingAt: leftChildIndex(parent: i)) {
return j
}
if let j = index(of: element, startingAt: rightChildIndex(parent: i)) {
return j
}
return nil
}0번 부터 시작해서 전체를 훑을 예정입니다. 외부에 노출된 메서드에는 시작 인자는 숨겨줄게요.
Array Building
지금 까지는 힙을 만들 때 insert값을 계속해서 전달해 주었는데요, 배열로 바로 초기화 할 수는 없을까요? 시도해봅시다.
init(sort: @escaping (T, T) -> Bool, elements: [T] = []) {
self.sort = sort
self.elements = elements
if !elements.isEmpty {
for i in stride(from: elements.count / 2 - 1, through: 0, by: -1) {
siftDown(start: i)
}
}
}elements를 받을 수 있도록 인자를 수정하고, elements를 전달 받은 다음 힙을 조건에 맞게 섞어? 줄게요
이 때 모든 값을 sift-down 할 필요는 없습니다. 중간에서 sift-down을 실시하면 됩니다. 비교 대상이 되는 부모 노드는 전체 노드의 절반 만큼만 존재하기 때문이죠!
이제는 아래 처럼 Heap을 만들 수 있습니다.
var heap = Heap<Int>(sort: >, elements: [1,7,3,2,6,8])
while let node = heap.remove() {
print(node)
}
//8
//7
//6
//3
//2
//1Performence
- remove: O(log n)
- insert: O(log n)
- search: O(n)
Reference.
'Data Structure' 카테고리의 다른 글
| Data Structure (0) | 2022.12.06 |
|---|

